L’image du chaos déterministe

diagramme de Feigenbaum passant du linéaire au chaos par quelques bifurcations
Le physicien Per Bak dans « Quand la nature s’organise » :
« La thèse de Feigenbaum était qu’à proximité de la transition vers le chaos, la dynamique devait être identique pour tous les systèmes passant à travers une séquence infinie de bifurcations avec doublement de période. Bien que la théorie de Feigenbaum reposât sur un modèle très grossièrement simplifié, elle fut magnifiquement confirmée par un grand nombre d’expériences sur des systèmes complexes (liquide soumis à des rouleaux convectifs tournants, oscillateur ou pendule poussé à un rythme régulier, ….). »

Le chaos déterministe, ni ordre, ni désordre,

Un monde dynamique non-linéaire aux frontières fractales

FRACTALES DE MANDELBROT ET DE JULIA

Mots clefs :

dialectique –
discontinuité –
physique quantique –
chaos déterministe –
système dynamique –
le temps -
non-linéarité –
émergence – rupture de symétrie –
inhibition –
boucle de rétroaction –
contradictions –
crise –
transition de phase –
auto-organisation – vide - révolution permanente - économie politique -
Blanqui -
Lénine -
Trotsky –
Barta -
Prigogine -
Gould

DANS LA NATURE : CROISSANCE PAR AGRÉGATION, PAR PERCOLATION

FOUGÈRE ET SON IMITATION PAR UNE FONCTION FRACTALE

FRONTIÈRE FRACTALE DANS UN PROCESSUS DE DIFFUSION

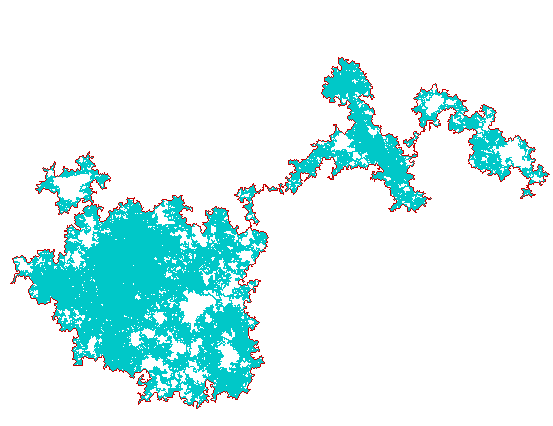
MOUVEMENT BROWNIEN

NUAGES OU INTERFACE DYNAMIQUE ET FRACTALE DES PHASES GLACE, LIQUIDE ET VAPEUR D’EAU DANS L’AIR

Site : Matière et révolution

www.matierevolution.fr

Sommaire du site

Pourquoi ce site ?

Chaos déterministe, le film

Pour nous écrire, cliquez sur Répondre à cet article

Pour lire cet article, cliquez sur :

L’image du chaos déterministe

– - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Lire également sur le site Matière et Révolution :

Le chaos déterministe

Chaos déterministe (dynamique non-linéaire) et dialectique - en anglais -

La dynamique chaotique de la géophysique et de la climatologie.

Climatologie et chaos déterministe.

Le cœur et le chaos déterministe

Le cerveau et le chaos déterministe

Psychanalyse et chaos déterministe

Chaos cardiaque, cérébral et cellulaire : les rythmes émergents du vivant

Qu’est-ce que le chaos déterministe en sciences ?

Lire à l’extérieur du site :

James Gleick expose le chaos déterministe

Le chaos dans les système inertes et vivants

Chaos en sciences ou les lois du désordre

La sensibilité aux conditions initiales et le chaos

Ilya Prigogine et Isabelle Stengers dans « Entre le temps et l’éternité » :

« Dans le passé, (…) tous les systèmes soumis à un attracteur semblaient devoir « se ressembler ». Aujourd’hui, la notion d’attracteur symbolise au contraire la diversité qualitative des systèmes dissipatifs.
La notion d’état attracteur renvoie en effet à celle de système dissipatif, producteur d’entropie. Un pendule idéal, sans frottement, n’a pas d’état attracteur, mais poursuit indéfiniment son mouvement d’oscillation. En revanche, le mouvement d’un pendule réel s’amortit progressivement. Dans le cas du pendule simple, l’existence de l’attracteur que constitue son état d’équilibre (au sens mécanique) permet de caractériser tout mouvement pendulaire réel en toute généralité, sans avoir besoin de le connaître dans sa particularité. Quelles que soient la vitesse et la position initiale du pendule, nous savons en effet comment nous pourrons le décrire si nous attendons assez longtemps : il finira par se trouver au repos dans sa position d’équilibre. De même, l’existence de l’attracteur que constitue l’état d’équilibre thermodynamique permet d’affirmer qu’une population de milliards de milliards de particules dans une enceinte isolée évoluera vers un état dont la description ne dépend plus que d’un petit nombre de paramètres observables, tels que température et pression.
Pour nous représenter l’attracteur, introduisons un espace dans lequel cet attracteur est plongé. Cet espace possèdera autant de dimensions qu’il faut de variables pour décrire l’évolution temporelle du système. Les états d’équilibre des systèmes dissipatifs correspondent par définition à des attracteurs ponctuels, représentés par un point de cet espace. C’est également le cas pour les systèmes proches de l’équilibre thermodynamique et soumis au théorème de production d’entropie minimum. Dans tous les cas, quelle que soit la préparation initiale du système, l’évolution de celui-ci sous des conditions aux limites données – pourra être représenté par une trajectoire menant du point représentant l’état initial vers le point attracteur. Celui-ci domine donc la totalité de l’espace. Tous les systèmes représentés par les mêmes variables indépendantes aux mêmes conditions aux limites « reviennent au même », connaissent le même destin.
La découverte loin de l’équilibre des comportements cohérents, telle l’ « horloge chimique », avec sa période temporelle bien déterminée, implique un premier élargissement de la notion d’attracteur. Ici, il ne s’agit plus d’un point mais d’une ligne. Cette fois, quelle que soit la situation initiale, le système évolue vers un « cycle limite ».
Un système caractérisé par un cycle limite reste un système prévisible, que l’on peut décrire de manière simple. (…)
Jusqu’à ces dernières années, on croyait que les seuls attracteurs possibles correspondaient à des variétés continues, telles que lignes, surfaces et volumes. Mais la découverte des « attracteurs étranges » a ouvert des nouvelles. Les attracteurs étranges ne sont pas caractérisés par des dimensions entières, comme une ligne ou une surface, mais par des dimensions fractionnaires. Ce sont ce que, depuis Mandelbrot, on appelle des variétés fractales. (…)
Jusqu’à il y a peu, l’existence d’un attracteur avait été synonyme de stabilité et de reproductibilité : retour au « même » malgré les perturbations, quelles que soient les particularités initiales. Aux nouveaux types d’attracteurs correspondent des comportements « sensibles aux conditions initiales » qui font perdre son sens à la notion de « même ». Dans toute région, aussi petite soit-elle, occupée par l’attracteur fractal, passent autant de trajectoires que l’on veut, et chacune de ces trajectoires connaît un destin différent des autres. En conséquence, des situations initiales aussi voisines que l’on veut peuvent engendrer des évolutions divergentes. La moindre différence, la moindre perturbation, loin d’être rendue insignifiante par l’existence de l’attracteur, a donc des conséquences considérables. (…)
Nous arrivons ici à la définition du comportement « chaotique », qui est un comportement typique des systèmes caractérisés par un attracteur étrange. Un comportement est chaotique si des trajectoires issues de points, aussi voisins que l’on veut dans l’espace des phases, s’éloignent les unes des autres au cours du temps de manière exponentielle ; la distance entre deux points quelconques appartenant à de telles trajectoires croit proportionnellement à une fonction exponentielle de l’inverse du temps de Lyapounov.
Le temps de Lyapounov permet de définir une véritable « échelle de temps ».